neural network
지난 시간까지 선형모델에 대해 알아봤다.
오늘은 비선형모델에 대해 알아보자.
신경망(neural network)은 선형모델과 비선형함수로 이루어진다.
앞서 배운 것을 다시 상기해보자면 아래 식과 같다.
\(y = XW + b\)
y: 출력 행렬, n x p
X: 입력 행렬, n x d
W: 가중치 행렬, d x p
b: 절편 행렬, n x p
여기서 절편 행렬은 같은 열이면 모든 행의 값이 다 같은 행렬이다.
즉, 하나의 p차원 벡터가 n개 복사하여 나타낸 행렬이다.
신경망은 출력 행렬 y의 각 값에 비선형함수를 적용함으로서 비선형모델이 된다.
이런 비선형모델을 단일 퍼셉트론(perceptron)이라 하며 여기서 사용한 비선형함수를 활성함수(activation function)이라 한다.
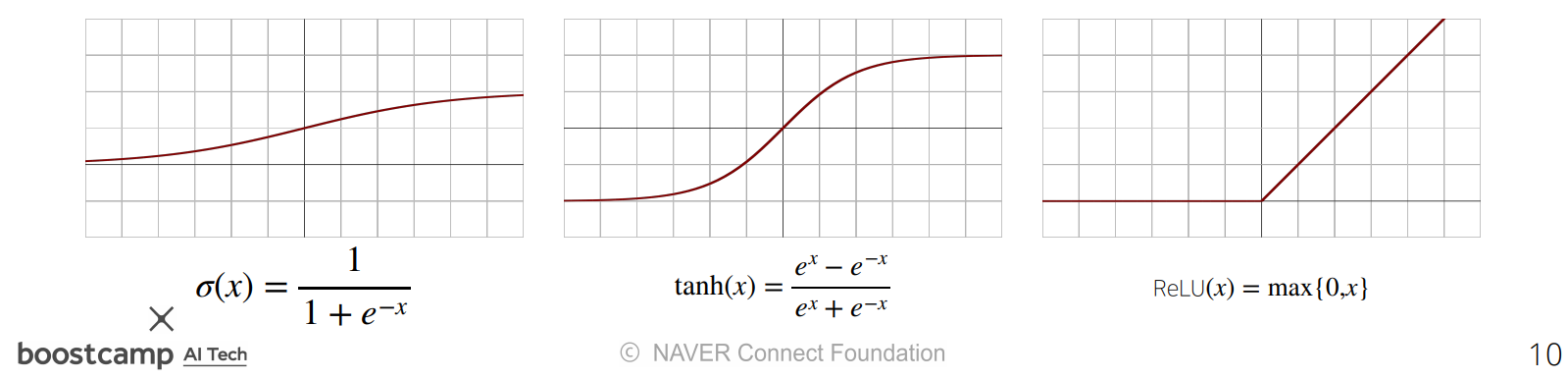
대표적인 활성함수를 살펴보면 다음과 같다.
좌측부터
sigmoid,hyperbolic tangent,ReLU(Rectified Linear Unit)
다층 퍼셉트론은 단일 퍼셉트론을 여러개 연결한 모델이다.
다음은 2층 퍼셉트론에 대한 예시이다.
\(y_1 = XW_1 + b_1\\
o_1 = f(y_1)\\
y_2 = o_1W_2 + b_2\\
o_2 = f(y_2)\)
$W_1, b_1$은 1층 퍼셉트론에 대한 가중치 행렬과 절편 행렬이다.
$f$는 활성함수이며 $o_1$은 출력 행렬 $y_1$에 활성함수를 적용한 행렬이다.
층마다 최종적으로 출력되는 행렬은 $o_1$와 같다.
다음 층에서는 이전 층의 결과 값인 $o_1$ 행렬을 입력으로 받는다.
$w_2, b_2$는 2층 퍼셉트론의 가중치 행렬과 절편 행렬로 1층의 것과는 다르다.
softmax
분류 모델에서 사용한다.
모델의 출력을 확률로 바꿔준다.
모델을 추론할때 softmax를 사용하지 않고 가장 큰 값을 선택해 one-hot 벡터로 바꾼다.
universal approximation theorem
신경망에서 히든 레이어와 비선형 활성함수를 사용하면 어떠한 연속함수에 근사할 수 있다??
사실 이 부분은 잘 모르겠다.
좀 더 공부한 후 수정할 예정이다.
그 밖에 내용
층이 깊을수록 적은 가중치로 복잡한 함수에 근사할 수 있다.
층이 얇으면 가중치의 숫자가 많아야 한다.
입력 행렬부터 출력 행렬까지 진행하는 것을 순전파(forward propagation)이라 한다.
가중치 학습을 위해 출력 행렬부터 입력 행렬까지 gradient를 계산하는 것을 역전파(back propagation)이라 한다.