Week02 Day09

하… 오늘 수업 장난없네…

probability

확률은 고전적 정의와 공리적 정의로 나뉜다.

고전적 정의는 어떤 사건의 발생 확률은 그것이 일어날 수 있는 경우의 수 대 가능한 모든 경우의 수의 비이다.
단, 이는 어떠한 사건도 다른 사건들 보다 더 많이 일어날 수 있다고 기대할 근거가 없을 때, 그러니까 모든 사건이 동일하게 일어날 수 있다고 할 때에 성립된다.¹

공리적 정의에서 확률은 다음 3가지를 만족한다.²

\[E : event, S: sample\ sapce\\ 1. P(E) \ge 0, P(E) \in \mathbb{R}, \mathbb{R}: real\ number\ set\\ 2. P(S) = 1\\ 3. P(\bigcup_{i=1}^\infty E_i) = \sum_{i=1}^\infty P(E_i)\]

probability theory

딥러닝은 수학 및 확률론에 기반한 이론이다.
입력 데이터 $X$와 출력 데이터 $y$가 있다고 하자.
그럼 데이터 공간을 $\mathscr{X} \times \mathscr{y}$ 이라고 표기하고 $\mathscr{D}$ 를 데이터 공간에서 데이터를 추출하는 분포라 하자.
데이터는 $(\mathscr{x}, \mathscr{y}) \thicksim \mathscr{D}$ 이라 표기한다.
이때 현실적으로 $\mathscr{D}$ 의 분포를 알기 어렵다.
확률변수는 확률분포 $\mathscr{D}$ 에 따라 이산형(discrete), 연속형(continuous)로 구분된다.
데이터 공간의 값들이 모두 실수라고 해서 연속형일 필요가 없다(이산형 확률변수로 생각해도 되는 경우가 있다).
주어진 데이터를 보고 원래 분포 $\mathscr{D}$ 를 모델링하며 이를 결합분포 $P(X, y)$ 라 한다.
이 결합분포는 $\mathscr{D}$ 의 분포와 상관없이 이산형 혹은 연속형으로 모델링할 수 있다.
이렇게 할 수 있는 이유는 주어진 데이터를 보고 컴퓨터로 원래 분포에 근사할 수 있는 방법들이 여러 존재하기 때문이다.
조건부확률분포 $P(X|y)$ 는 $X$ 와 $y$ 사이의 관계를 모델링한다.
분류 문제에서 $P(y|X)$ 는 입력 데이터 $X$ 가 주어질때 출력이 $y$ 일 확률을 의미한다.
딥러닝에서는 입력 데이터와 가중치 행렬 $W_1, W_2, …$ 을 softmax의 입력값으로 하여 분류 클래스의 확률을 구한다.
회귀 문제에서 확률밀도함수의 값은 확률을 의미하지 않으며 기대값을 구해야 한다.
즉, 조건부기대값 $E(y|X) = \int_yyP(y|X)dy$ 를 구해야 한다.

범함수(functional)

준비중…

the Law of unconscious statistician

준비중…

monte carlo method

난수를 이용하여 함수의 값을 확률적으로 계산하는 알고리즘을 부르는 용어이다.³

확률의 정의를 이용하여 기하적인 확률의 정의를 한다면 표본공간 $S$ 가 평면의 영역이라 하고 $S$ 안에 사건들이 일어날 가능성이 모두 같다면 사건 $A$ 의 확률은 $\frac{A의 영역의 넓이}{S의 영역의 넓이}$ 이다.
예를 들어 몬테 카를로 방법으로 원주율(pi)를 구해보자.
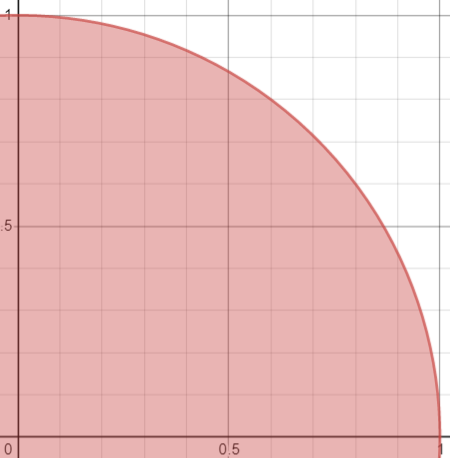
그러기 위해 그래프 $X^2+Y^2 \le 1, 0 \le x \le 1, 0 \le y \le 1$를 생각해보자.

위 그래프에서 임의의 $0 \le x \le 1, 0 \le y \le 1$ 인 $(x, y)$ 중 붉은색 영역에 있을 확률을 구할 것이다.

먼저 $0 \le x \le 1, 0 \le y \le 1$ 인 난수 $n$ 개를 생성한다.
생성된 난수와 원점간의 거리를 구하여 1보다 작은 점의 갯수 $a$ 를 구한다.
기하적 확률 정의에 의해 여기서 표본공간 $S$ 는 $0 \le x \le 1, 0 \le y \le 1$ 가 되며 이 영역의 넓이는 1이다. 사건 $A$ 의 영역의 넓이는 $\frac{\pi}{4}$ 이므로 확률은 $\frac{\frac{\pi}{4}}{1} = \frac{\pi}{4}$ 이다.
또한 확률의 정의에 의해 $\frac{사건 A에서 발생한 횟수}{표본공간 S에서 발생한 사건의 횟수} = \frac{a}{n}$ 이다.

$n$ 이 커질수록 실제확률에 근사할 것이다. 따라서 $\pi \simeq \frac{4a}{n}$ 로 근사할 수 있다.

import numpy as np
def approximate_pi(n):
  arr = np.random.uniform(0, 1, size=(n, 2))
  distances = np.square(arr).sum(axis=1)
  a = (distances < 1).sum()
  return 4 * a / n
print(approximate_pi(1000)) # 3.092
print(approximate_pi(10000)) # 3.1456
print(approximate_pi(100000)) # 3.14676
print(approximate_pi(1000000)) # 3.142392

그럼 몬테 카를로 방법이 딥러닝에서 어떻게 쓰일까?
다음과 같은 상황을 보자.
$\mathbb{E}_{x \sim P(X)}[f(X)] = \int_xf(X)P(X)dx$
대부분의 상황에서 확률분포 $P(X)$ 가 어떤 분포인지 모르며 주어진 데이터가 분포에서 일부분 추출된 것일 수 있다.
그래서 몬테 카를로 방법에 의해 다음과 같이 근사할 수 있다.
$\mathbb{E}_{x \sim P(X)}[f(X)] \simeq \frac{1}{n}\sum_{i=1}^Nf(X_i)$
이 방법의 특징은 모든 수를 계산하지 않아도 실제 값에 근사할 수 있어서 계산 비용이 줄어든다.

이전Week02 Day08

다음Week02 Day10