왕밤빵

Week03 Day11

 
  • 2021년 02월 01일

하 밀렸다…
3주차 과정이 다 끝난 다음에 작성했다…

conditional probability

결합확률(joint probability) $P(A, B)$ 은 사건 A와 B를 둘다 고려한 확률이다.
조건부확률(conditional probability) $P(A|B)$ 는 사건 B를 고려한 A에 대한 확률이다.
얼핏보면 둘다 사건 A, B가 동시에 일어난 확률을 구하는 것 같다.
나는 이 둘의 차이를 다음과 같이 구분한다.

remind: 확률의 고전적 정의
The probability of an event is the ratio of the number of cases favorable to it, to the number of all cases possible when nothing leads us to expect that any one of these cases should occur more than any other, which renders them, for us, equally possible.1

\(P(A, B) = \frac{n(A, B)}{n(S)}\\ P(A|B) = \frac{n(A, B)}{n(B)}\\ n(S): 전체\ 사건의\ 경우의\ 수\\ n(B): 사건\ B가 일어난\ 경우의\ 수\\ n(A, B): 사건\ A와\ B가\ 동시에\ 일어난\ 경우의\ 수\)
위 정의에 의해 두 확률의 공통점은 분자($n(A, B)$) 가 동일하다.
차이점으로 $P(A, B)$ 는 사건 A와 B 둘다 발생하던지 아니던지 즉, 모든 경우의 수를 고려했고 $P(A|B)$ 는 사건 B가 발생한 것만 고려했다.
또한 $P(A|B)$ 와 $P(A)$ 를 비교하고 싶다.
$P(A)$ 는 사건 A에 대한 확률이다.
$P(A|B)$ 는 사건 B에 대한 정보가 주어져서 A에 대한 확률을 다시 구하는 것이다.

Bayes theorem

베이즈 정리란 두 확률변수의 사전 확률과 사후 확 사이의 관계를 나타내는 정리이다.2
수식은 다음과 같다.
\(P(A|B) = \frac{P(B|A)P(A)}{P(B)}\\ P(A): A의\ 사전\ 확률\\ P(A|B): B에\ 대한\ 정보가\ 주어질때\ A의\ 사후\ 확률\\ P(B|A) = L(A|B): B가\ 주어질때\ A의\ 가능도(likelihood)\\ P(B): B의\ 사전\ 확률\ 혹은\ 정규화\ 상수\ 혹은\ evidence\)
$P(A|B)$ 직접 구할 수 없고 $P(B|A)$ 을 알고 있을때 베이즈 정리를 이용하여 구할 수 있다.
위 조건부확률을 이용하면 베이즈 정리가 어렵지 않다.
하지만 베이즈 정리에 사용되는 값들, $P(A), P(B), P(B|A)$, 의 의미를 이해하는 게 어려웠다, 가능도, 사전 확률 …
$P(B)$ 가 이산확률이라면 $P(B) = \sum_i P(B \cap A_i)$ 처럼 나타낼 수 있다.
또한 결합확률은 조건부확률의 정의에 따라 $P(B) = \sum_i P(B \cap A_i) = \sum_i P(A_i)P(B|A_i)$ 로 나타낼 수 있다.

베이즈 정리는 조건부확률을 이용하여 확률을 갱신할 수 있다.
즉, $B$ 라는 새로운 정보가 주어질때 $P(A)$ 로부터 $P(A|B)$ 를 계산할 수 있다.

강의에 나온 문제를 풀어보자.

COVID-99의 발병률이 10%로 알려져 있다. COVID-99에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오 검진될 확률이 1%라고 할 때 양성판정일 때 정말로 COVID-99에 감염되었을 확률은?

\(P(COVID) = 0.1, COVID-99에\ 걸릴\ 확률\\ P(D|COVID) = 0.99, COVID-99에\ 실제로\ 걸렸을\ 때\ 검진될\ 확률\\ P(D|COVID^c) = 0.1, 걸리지\ 않았는데\ 검진될\ 확률\)
구하는 것은 진단결과 양성판정일 때 COVID-99에 걸릴 확률로 $P(C|D)$ 를 구하는 것과 같다.
직접적으로 $P(C|D)$ 를 구할 수 없으나 사전 확률과 가능도가 주어졌으므로 베이즈 정리를 이용한다.

\(P(COVID|D) = \frac{P(D|COVID)P(COVID)}{P(D)}\\ \qquad = \frac{P(D|COVID)P(COVID)}{P(D \cap COVID) + P(D \cap COVID^c)}\\ \qquad = \frac{P(D|COVID)P(COVID)}{P(COVID)P(D|COVID) + P(COVID^c)P(D|COVID^c)}\\ \qquad = \frac{0.99*0.1}{0.99*0.1+0.1*0.9} \backsimeq 0.523\)
그럼 두번 검진해서 양성판정일 때 실제로 걸렸을 확률은 어떻게 구할까?
앞서 설명했듯이 베이즈 정리는 정보를 갱신하여 확률을 구할 수 있다고 했다.
그럼 기존 정보를 활용하여 계산해보면 $P(COVID|D)$ 가 $P(COVID)$ 로 갱신된다.
그러면 $\frac{0.99 * 0.523}{0.99 * 0.523 + 0.1 * 0.477} \backsimeq 0.915$ 가 된다.

confusion matrix

a confusion matrix is a specific table layout that allows visualization of the performance of an algorithm.3

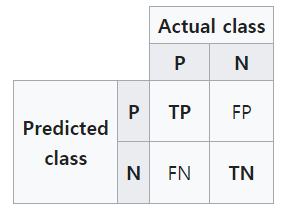
confusion matrix는 2개의 class를 다루는 분류 문제에서 알고리즘의 성능을 표로 시각화한 것으로 다음과 같다.

TP(True Positive): 예측한 값아 True, 실제 값이 True인 경우
FP(False Positive): 예측한 값이 True, 실제 값이 False인 경우
FN(False Negative): 예측한 값이 False, 실제 값이 True인 경우
TN(True Negative): 에측한 값이 False, 실제 값이 False인 경우

4
이 표에서 얻을 수 있는 몇가지 척도를 소개한다.

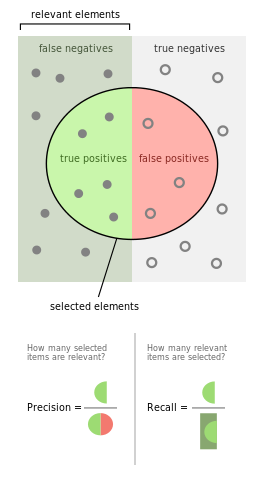
  • sensitivity or recall or TPR(true positive rate) = $\frac{TP}{TP + FN}$
    실제 True 중 True로 예측한 비율
  • precision or PPV(positive predictive value) = $\frac{TP}{TP + FP}$
    예측한 True 중 실제 True인 비율
  • accuracy = $\frac{TP + TN}{TP + FP + FN + TN}$
    전체 경우 중 예측과 실제가 일치하는 비율
  • F1 score = $\frac{2recallprecision}{recall + precision}$
    높을수록 좋은 알고리즘이다.
    accuracy로 알고리즘의 성능을 평가하기 어려운 경우가 있다.
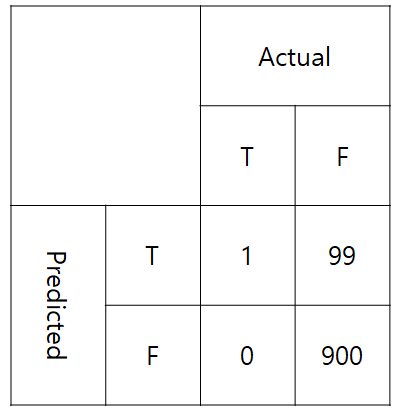
    예를 들어 confusion matrix가 다음과 같다면 accuracy와 F1 score를 비교해보자.

    accuracy = $\frac{900 + 1}{900 + 0 + 99 + 1} = 0.901$
    precision = $\frac{1}{99 + 1} = 0.01$
    recall = $\frac{1}{1 + 0} = 1$
    F1-scroe = $\frac{2 * 0.01 * 1}{0.01 + 1} \backsimeq 0.019$
    위와 같은 경우는 분류할 class가 unbalanced 하다.
    accuracy만 보고 알고리즘의 성능을 평가하면 안되는 예를 보여준다.

good deep learner?

  • implementation(Tensorflow, Pytorch)
  • mathematics(linear algebra, probability)
  • recent paper

artificial intelligence


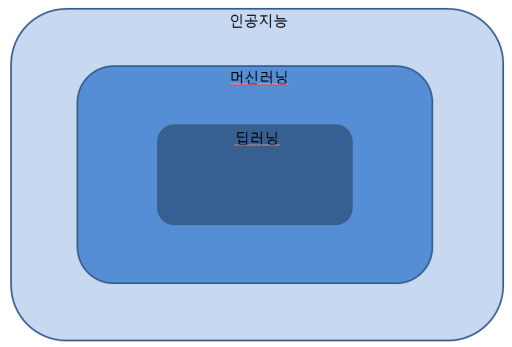
인공지능: 인간의 지능을 모방하는 것.
머신러닝: 우리가 학습하고 싶은 것은 데이터 안에 있다(Data-Driven Approach).
딥러닝: 머신러닝 방법 중 신경망을 사용.

neural network

neural networks are computing systems vaguely inspired by the biological neural networks that constitute animal brains.5

신경망은 동물의 뇌를 구성하는 생물학적 신경망에 애매모호하게 영향을 받은 컴퓨팅 체계이다.
많은 사람들이 신경망이 왜 잘되는가에 대한 물음에 대답으로 동물의 뇌를 모방했기 때문이다 라고 한다.
instructor는 신경망이 잘되는 이유가 동물의 뇌를 모방했기 때문이라는 것과는 다른 의견이 있었다.
6
예를 들어 과거의 사람들은 하늘을 날고 싶어서 새가 날아가는 모습을 모방하여 그와 비슷한 것을 만들었다.
7
하지만 시대가 발전하면서 새의 모양과 달라지면서 위와 같은 모습으로 진화했다.
여기서 하고 싶은 말은 인간의 뇌를 모방하여 신경망을 만들었지만 현재의 딥러닝은 인간의 뇌를 모방했다고 말하기 어렵다.
신경망이 잘되는 이유가 인간의 뇌를 모방했기 보다는 수학적으로 접근하는게 맞다고 언급했다.

간단한 예시로 선형회귀모델을 생각해보자.
데이터가 주어지고 선형회귀모델을 만들었다.
그리고 실제와 예측간의 차이를 나타내는 손실함수도 정의했다.
손실함수를 최소화하기 위해 gradient를 구하여 parameter를 update한다.
이때 gradient는 아주 작은 근방에서만 유효하기 때문에 parameter를 아주 조금씩 update해야 한다.
update를 조절하는 역할을 learning rate라 한다.

universal approximation theory

hidden layer 하나 있는 신경망은 대부분의 measurable 함수에 근사할 수 있다.
이 말은 그러한 신경망이 존재한다는 것이지 어떻게 찾는지는 설명하지 않는다.
더 자세하게 알아보기

딥러닝의 핵심 요소

  • 데이터: 우리가 풀고자 하는 문제는 데이터에 의존한다.
  • 모델: 같은 데이터라도 모델에 따라 성능이 달라진다.
  • 손실함수: 모델의 예측과 실제가 얼마나 차이나는지를 정량화한 함수.
  • 최적화: 손실함수를 줄이기 위해 모델을 수정하는 알고리즘.

historical review

  • 2012 - AlexNet
    최초로 딥러닝 모델을 사용하여 이미지 인식 대회에서 우승하였다.
    이전에는 ML 모델이 강세였고 이후 ML 모델이 딥러닝 모델을 이긴 경우가 없다.
  • 2013 - DQN
    Q-learning 이라는 강화학습 기법에 딥러닝을 적용하였다.
  • 2014 - Encoder / Decoder
    한 문장을 다른 문장으로 바꿔준다.
    이 모델로 기계번역의 트렌드가 바뀌었다.
  • 2015 - GAN(Generative Adversarial Network) 생성 모델 트렌드의 변화를 일으켰다.
  • 2015 - ResNet(Residual Neural Network)
    신경망을 깊게 쌓으면 학습이 잘 안되는 현상을 해결해주었다.
    이 모델을 계기로 좀 더 깊게 쌓은 모델이 생겼다.
  • 2017 - Transformer 기존 RNN 모델보다 성능이 더 좋다.
  • 2018 - BERT(Bidirectional Encoder Representations from Transformers)
    이 모델 등장 후 fine-tuned model에 대한 개념이 중요해졌다.
  • 2019 - GPT-3(Generation Pre-trained Transformer-3)
    NLP 모델이며 굉장히 많은 parameter를 갖고 있다.
  • 2020 - self supervised learning
    label이 없는 데이터를 사용하여 학습 방법

pytorch 입문

numpy 구조를 가지는 Tensor 객체.
자동미분을 지원한다.

import torch
import numpy as np
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
x_numpy = np.random.rand(2,784)
x_torch = torch.from_numpy(x_numpy).float().to(device)
x_torch = x_torch.detach().cpu().numpy()

pytorch는 위와 같이 특정 device를 지정하여 사용할 수 있다.
학습하기 위해서는 memory에 있는 데이터를 device가 있는 memory에 올려야 학습이 가능하다.
x_numpy의 datatype은 float64이다.
Tensor 객체로 바꾼 후 float()을 통해 float32로 바꾸고 device에 데이터를 보낸다.
detach()는 Tensor 객체가 연산들을 추적하는 것을 멈추게 한다.
Tensor 객체는 기본적으로 연산들을 기록했다가 backward()가 호출되면 gradient를 계산한다.
추적하는 것을 막고 cpu()를 통해 gpu memory에서 memory로 객체를 옮긴다.
혹은 with torch.no_grad(): 이하에 코드를 넣으면 추적하지 않게 한다.

class MultiLayerPerceptronClass(nn.Module):
    def __init__(self, name='mlp', xdim=784, hdim=256, ydim=10):
        super(MultiLayerPerceptronClass, self).__init__()
        self.name = name
        self.xdim = xdim
        self.hdim = hdim
        self.ydim = ydim
        self.lin_1 = nn.Linear(
            xdim, hdim
        )
        self.lin_2 = nn.Linear(
            hdim, ydim
        )
        self.init_param() # initialize parameters

    def init_param(self):
        nn.init.kaiming_normal_(self.lin_1.weight)
        nn.init.zeros_(self.lin_1.bias)
        nn.init.kaiming_normal_(self.lin_2.weight)
        nn.init.zeros_(self.lin_2.bias)

    def forward(self, x):
        net = x
        net = self.lin_1(net)
        net = F.relu(net)
        net = self.lin_2(net)
        return net

M = MultiLayerPerceptronClass(name='mlp', xdim=784, hdim=256, ydim=10).to(device)
loss = nn.CrossEntropyLoss()
optm = optim.Adam(M.parameters(), lr=1e-3)

model을 만드려면 여러 방법이 있다.
그 중 앞으로 nn.Module을 상속하여 class 형태로 만들 것이다.
class 형태로 모델을 만드려면 반드시 nn.Module을 상속해야 한다.
model 역시 device로 보내야 된다.

M.init_param() # parameter를 초기화 한다.
M.zero_grad() # 이전의 gradient가 남아있다. 매번 학습할때마다 reset해줘야 한다.
loss_out = loss(y_pred, batch_out.to(device))
loss_out.backward() # loss를 계산하고 이에 대한 gradient를 계산한다.
optm.step() # optimizer를 통해 weight를 update한다.

  1. 위키피디아 - 확률의 고전적 정의 ↩

  2. 위키피디아 - 베이즈 정리 ↩

  3. 위키피디아 - confusion matrix ↩

  4. 위키피디아 - F1 score ↩

  5. 위키피디아 - 인공신경망 ↩

  6. 위키피디아 - avion-3 ↩

  7. 위키피디아 - F-22 ↩

검색