sequential data
$x_1,\ …,\ x_n$ 시퀀스 데이터들은 i.i.d(independent, identical distribution) 조건을 만족하지 않는다.
$x_n$ 은 이전의 데이터 $x_1,\ …,\ x_{n-1}$ 에 영향을 받고 $x_{n+1}$ 은 $x_1,\ …,\ x_n$ 에 영향을 받는다.
즉, 순서를 바꾸거나 과거 정보에 손실이 확률분포에 영향을 준다.
소리, 문자열, 주가 등의 데이터가 시퀀스 데이터에 해당한다.
$x_1,\ …,\ x_n$ 에 대한 확률을 고려해보자.
$P(x_1,\ …,\ x_n)$ 은 다음처럼 조건부확률을 이용할 수 있다.
\(P(x_1,\ ...,\ x_n) = P(x_n|x_1,\ ...,\ x_{n-1})P(x_1,\ ...,\ x_{n-1})\\
\qquad \qquad \qquad \ = P(x_n|x_1,\ ...,\ x_{n-1})P(x_{n-1}|x_1,\ ...,\ x_{n-2})P(x_1,\ ...,\ x_{n-2})\\
\qquad \qquad \qquad \ = \prod^n_{t=1}P(x_t|x_1,\ ...,\ x_{t-1})\)
이전 데이터로 앞으로 발생할 데이의 확률분포를 구하기 위해 다음과 같이 조건부확률을 이용할 수 있다.
\(x_n \sim P(x_n|x_1,\ ...,\ x_{n-1})\)
확률분포를 구하기 위해 과거의 데이터를 사용하지만 모든 데이터를 사용할 필요없다.
예를 들어 오늘의 주가를 예측하기 위해 이전 20년치의 데이터가 필요할까?
이전 n-1개의 데이터로 $x_n$ 의 확률분포를 구했다면 $x_{n+1}$ 의 확률분포는 $x_n$ 을 포함한 n개의 데이터로 구한다.
조건부확률에서 조건의 길이가 변한다.
즉, 시퀀스 데이터를 다룬다는 것은 가변적인 데이터를 다룬다는 것이다.
autoregressvie model은 이전 데이터 중 정해진 길이만큼 사용하여 확률분포를 구한다.
하지만 길이를 어떻게 정해야 할지 문제이다.
바로 이전의 데이터만 고려하는 모델을 1차 markov model이라 하며 다음과 같다.
\(P(x_1,\ ...,\ x_n) = P(x_n|x_{n-1})P(x_{n-1}|x_{n-2})...P(x_2|x_1)P(x_1)\\
\qquad \qquad \qquad \ = \prod^n_{t=1}P(x_t|x_{t-1})\)
latent autoregressvie model은 이전 데이터를 요약한 잠재변수 H를 이용한다.
\(x_n \sim P(x_n|h_{n-1},\ x_{n-1}),\ h_{n-1} = f(H_{n-2},\ x_{n-2})\)
이렇게 한다면 다루는 데이터가 고정 길이로 바뀌어 확률분포를 구할 수 있다.
이런 모델을 RNN이라 한다.
RNN(Recurrent Neural Network)
이전에 배운 MLP로 표현한다면 다음과 같다.
\(O = HW^{(2)}+b^{(2)}\\
H = \sigma(XW^{(1)} + b^{(1)})\\
H:\ latent\ variable\\
W:\ weight\\
b:\ Bias\)
위 모델은 잠재변수를 표현했지만 과거 데이터를 고려하지 않은 모델이다.
그래서 다음과 같이 바뀌어야 한다.
\(O_n = H_nW^{(2)}+b^{(2)}\\
H_n = \sigma(X_nW^{(1)} + b^{(1)} + H_{n-1}W^{(3)})\)
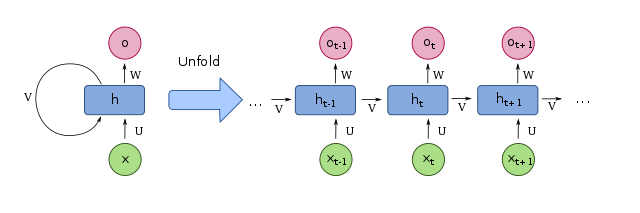
이것이 가장 기본적이고 MLP와 유사한 vanilla RNN이다.
MLP는 각 layer의 weight가 각각 따로 존재하지만 RNN의 weight는 n과 상관없이 일정하다.
 1
1
위 그림은 RNN을 나타낸다.
RNN의 backpropagation을 BPTT(Backpropagation Through Time)이라 부른다.
BPTT 수식 나중에 추가
$h_{n}$ 의 gradient는 $o_n$ 의 gradient와 $h_{n+1}$ 의 gradient로 이루어 진다.
시퀀스의 길이가 길수록(n이 커질수록) vanishing 혹은 exploding gradient가 발생한다.
exploding gradient가 발생할 수 있기 때문에 activation function으로 ReLU를 잘 사용하지 않는다.
마지막 시퀀스에서 처음까지 gradient를 계산하지 말고 일정 길이마다 gradient를 계산하는 것으로 해결할 수 있다.
이런 문제로 vanilla RNN으로 길이가 긴 시퀀스를 다루기 힘들다.
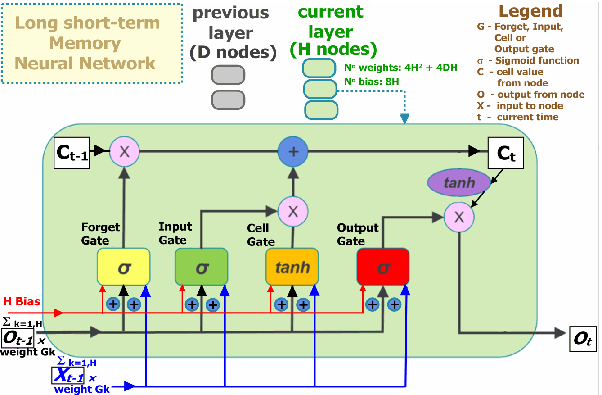
LSTM(Long-Short Term Memory)
vanilla RNN은 마지막 출력으로부터 가까운 시퀀스에 대한 데이터 정보(Short Term)는 잘 저장한다.
하지만 그로부터 멀어질수록 처음 데이터에 대한 정보(Long Term)를 유지하기 힘들다.
 2
2
위 그림은 LSTM의 구조를 나타낸다.