또 밀림…ㅋㅋ…
부스트캠프의 강의와 cs224n - Transformers를 참고하였다.
seq2seq with attention limitation
이전 강의에서 many-to-many 모델의 한 종류인 seq2seq with attention 을 살펴봤다.
seq2seq는 encoder, decoder가 RNN 이다.
RNN 모델의 한계가 있다.
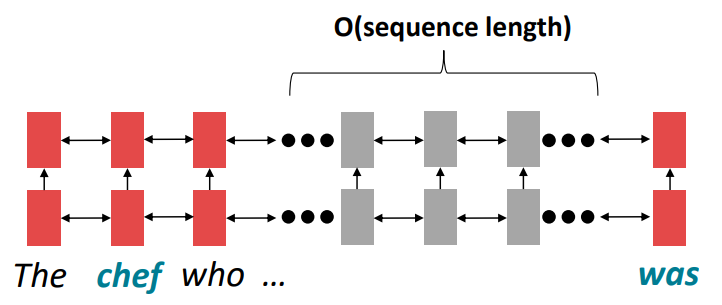
이 모델은 왼쪽에서 오른쪽으로 정보가 흐른다.
다시 말해, 선형적인 locality를 encoding한다.
가까이 있는 단어끼리 영향을 준다는 뜻이다.
문제는 멀리 떨어져 있는 단어가 정보를 주고 받으려면 O(N; sequence length)의 time step이 필요하다.
먼 거리에 있는 단어들은 gradient 문제로 인해 관계를 학습하기 힘들다.
문장을 이해하기 위해서 단어의 선형적인 순서를 고려하는 것은 올바른 방법이 아니다.
위 그림을 보면 chef와 was의 관계는 유의미하지만 chef의 정보가 was로 전해지기 위해 여러 time step이 필요하다.
즉, 왼쪽에서 오른쪽 혹은 역방향으로 정보가 흐르기 위해서는 O(sequence length)가 걸리고 병렬적으로 계산할 수 없다.
GPU는 한번에 수많은 독립적인 연산을 할 수 있다.
하지만 RNN은 이전 결과값이 없으면 다음 값을 계산할 수 없다.
이것은 대용량 데이터를 학습하기 어렵게 한다.
문제점을 정리하자면 다음 2가지로 요약할 수 있다.
- long-term dependency
- unparallelizable operation
위와 같은 이유로 sequential computation을 줄이기 위해 recurrent를 대체할 구조를 찾는다.
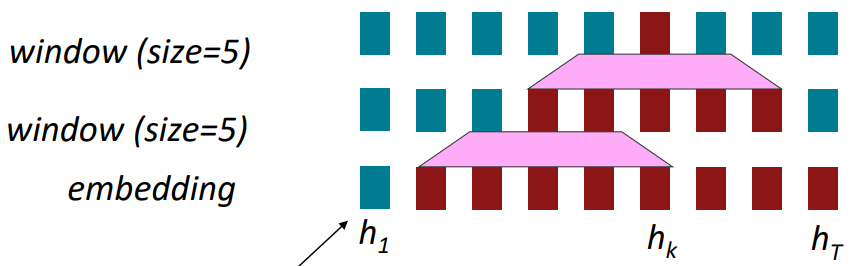
아래 그림처럼 kernel 크기가 5인 1차원 convolution을 생각해보자.
위 그림은 붉은색은 $h_k$ 와 상호작용하는 state들을 나타내며 embedding 위에 두 개의 convolution layer를 쌓은 모습이다.
convolution은 local context를 얻을 수 있다.
long-term dependency는 개선이 되는가?
convolution layer를 늘려서 receptive field를 넓히게 하여 먼 거리에 있어도 단어 간 상호작용을 할 수 있다.
다른 방법으로 attention을 사용하는 건 어떨까?
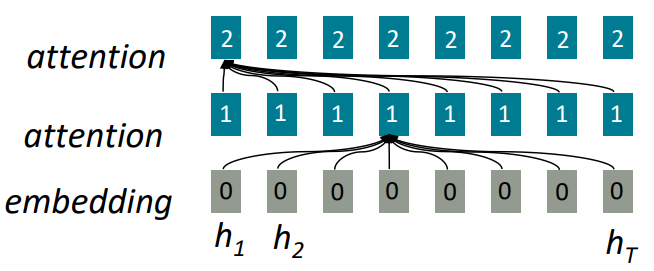
attention은 임의의 정보들 중 어떤 것에 접근하고 취합하는 것을 가능하게 한다.
위 그림을 보면 embedding 위에 attention layer 2개가 쌓여 있다.
또한 attention의 모든 embedding은 이전 layer의 모든 단어들과 상호작용한다.
만약 GPU의 core 수가 많다면 이 과정을 O(1)에 계산할 수 있다.
즉, sequence 길이와 상관없이 O(1)에 계산할 수 있다.
새로운 attention mechanism, self-attention을 소개한다.
self-attention
Self-attention, sometimes called intra-attention is an attention mechanism relating different positions of a single sequence in order to compute a representation of the sequence.1
self-attention은 sequence에 대한 representation을 얻기 위해 sequence의 다른 위치의 단어들을 고려한 방법이다.
seq2seq with attention에서는 query와 value를 정의했다.
여기서는 key라는 것을 추가했다.
sequence length $T$ 에 대해 query, key, value는 다음과 같다.
\(query: q_1,\ q_2,\ ...,\ q_T,\ q_i \in \mathbb{R^d}\\
key: k_1,\ k_2,\ ...,\ k_T,\ k_i \in \mathbb{R^d}\\
value: v_1,\ v_2,\ ...,\ v_T,\ v_i \in \mathbb{R^d}\\
output\ of\ previous\ layer: x_1,\ x_2,\ ...,\ x_T,\ x_i \in \mathbb{R^d}\)
query, key, value는 같은 source로부터 얻는다.
이 때문에 self-attention이라는 이름으로 불린다.
예를 들어 dot-product attention을 계산한다면 $q_i = k_i = v_i = x_i$ 가 된다.
이 경우 모두 같은 vector를 사용한다.
그러면 attention score는 $e_i = q^T_ik_j \in \mathbb{R}$ 이다.
softmax를 취한 후 $v_i$ 와 가중합을 계산한다.
그리고 self-attention를 여러 개 쌓는다.
그럼 이 방법이 recurrent 모델보다 더 좋은가?
그렇지 않다.
여러가지 문제가 있는데 문제점을 하나씩 나열하면서 그에 대한 해결책을 소개한다.
positional encoding
self-attention은 순서를 고려하지 않는다.
sequence 데이터는 순서가 중요한 의미를 갖는다.
그래서 순서를 고려한 방법을 소개한다.
나중에 추가…
Feedforward network
또다른 문제가 있다.
self-attention에는 non-linearity가 없다.
이를 추가하는 방법을 소개한다.
아래 그림처럼 self-attention의 출력값에 FFN(Feedforward Network)를 통과시켜 non-linearity를 추가할 것이다.
수식은 다음과 같다.
\(m_i = W_2ReLU(W_1 \times output_i + b_1) + b_2\)
같은 layer이면 동일한 $W_1, b_1, W_2, b_2$ 를 self-attention의 output에 동일하게 적용한다.
layer마다 새로운 parameter를 사용한다.
transformer
먼저 query, key, value에 대해 좀 더 알아보자.
${x_1,\ x_2,\ …,\ x_T }; x_i \in \mathbb{R^{d_1}}$ 를 transformer encoder의 input이라 하자, $T$ : sequence 길이.
그럼 query, key, value를 다음과 같이 정의하자.
$q_i = Qx_i,\ Q \in \mathbb{R^{d_2 \times d_1}}$, $Q$: query 행렬
$k_i = Kx_i,\ K \in \mathbb{R^{d_2 \times d_1}}$, $K$: key 행렬
$v_i = Vx_i,\ V \in \mathbb{R^{d_2 \times d_3}}$, $V$: value 행렬
이렇게 정의하면 $Q, K, V$ 행렬들이 $x_i$ 가 3가지 역할하는데 사용될 수 있다.
attention을 공부하면서 많이 어려웠던 부분은 그래서 query, key, value가 뭔데? 였다.
뜬금없이 query, key, value가 등장한 것 같아서 이해하기 어려웠다.
그래서 이것들에 대한 유래? 혹은 이것들이 갖고 있는 의미?를 찾기위해 구글링했고 아래 답변을 찾았다.
query, key, value의 concept은 정보검색(retrieval information)에서 왔다.
예를 들어 내가 youtube에서 어떤 비디오를 찾고 있다.
youtube은 db에서 후보가 되는 비디오의 정보(key)와 내가 찾는 비디오(query)를 비교하여 가장 유사한 비디오(value)를 보여준다.
multi-headed attention
만약 $q_i$ 와 $k_j$ 의 내적 값이 크다면 softmax 값은 다른 값들 보다 월등히 클 것이다.
즉, 문장의 어느 한 부분만 보겠다는 뜻이다.
한번에 문장의 여러부분을 보기 위해 attention을 여러번 하면 된다.
단, attention을 여러 layer 쌓는게 아니라 한 layer에서 병렬적으로 문장의 여러부분을 보겠다는 것이다.
이 방법을 multi-headed attention이라 한다.
이론적으로는 이전에 설명한 dot-product attention과 동일하지만 구현할 때 약간 차이가 있다.
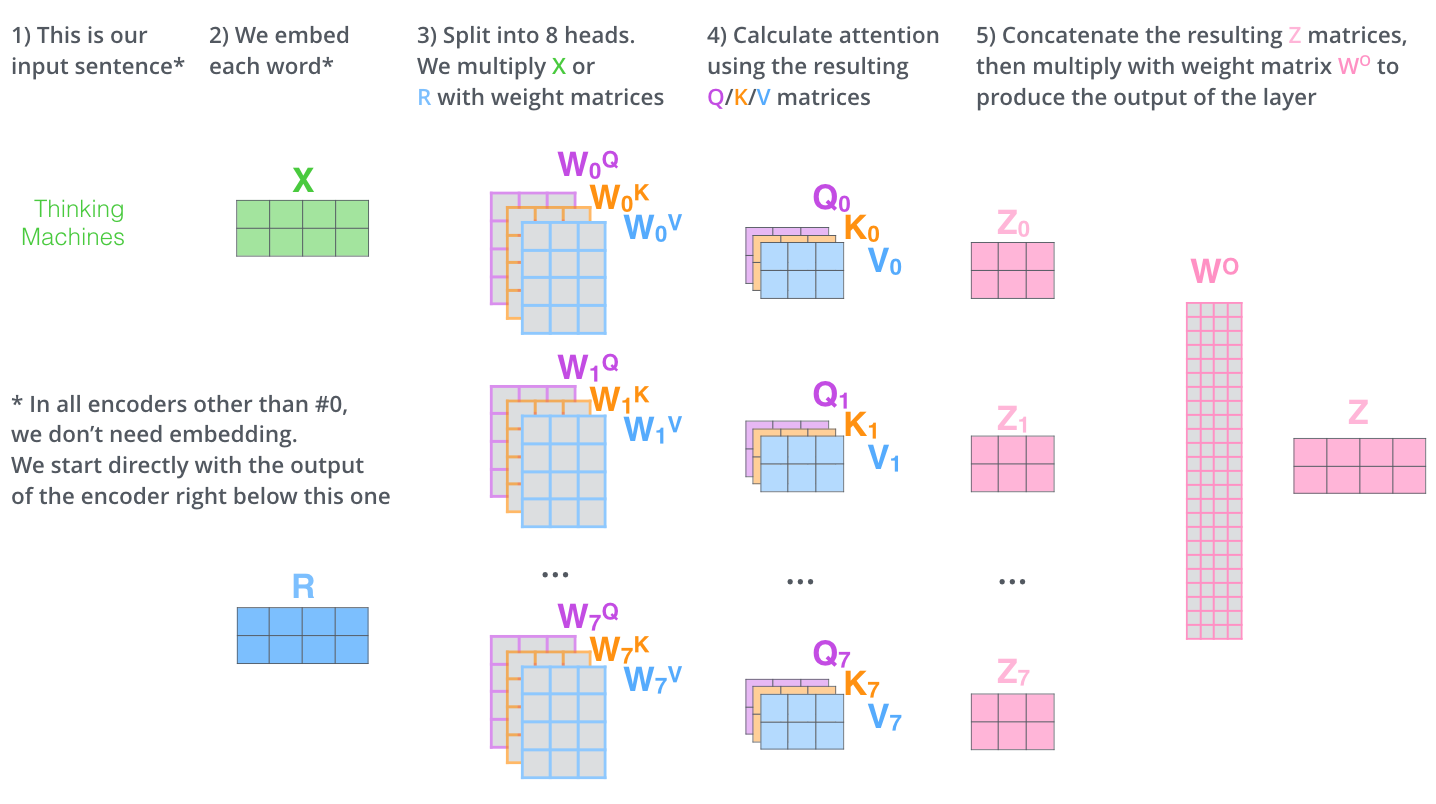
$Q_l,\ K_l,\ V_l \in \mathbb{R^{d_2 \times d_4}}$ 에서 $Q_l,\ K_l,\ V_l$ 은 $l$ 번째 head attention의 query, key, value 행렬이며 총 $h$ 개의 attention head가 있다고 하자.
attention output은 $output_l \in \mathbb{R^{d_4}}$ 이 된다.
그럼 모든 head에서 나온 output을 concatenation을 하고 선형변환을 한다.
선형변환은 차원을 바꿔주는 역할도 있지만 각 head에서 추출한 정보를 취합하는 역할도 한다.
output = $Y[output_1;output_2;…;output_h],Y \in \mathbb{R^{d_1 \times (h * d_4)}}$
아래 그림은 위 설명을 시각화한 것이다.
 2
2
While one attention head attends to the tokens that are relevant to each token, with multiple attention heads the model can learn to do this for different definitions of “relevance”.
For example there are attention heads that, for every token, attend mostly to the next word, or attention heads that mainly attend from verbs to their direct objects.3
위키피디아에 따르면 하나의 attention head가 각 token과 관련이 있는 token에 주목하는 동안, 모델은 여러 attention head를 사용하여 “관련성”의 다른 정의들에 대해 관련있는 token에 주목하는 법을 배울 수 있다.
예를 들어 모든 token에 대해 주로 다음단어에 주목하거나 동사부터 목적어까지 주목하는 attention head가 있다.
tricks for transformer
나중에 추가…
- residual connection
- layer normalization
- scaled-dot product attention
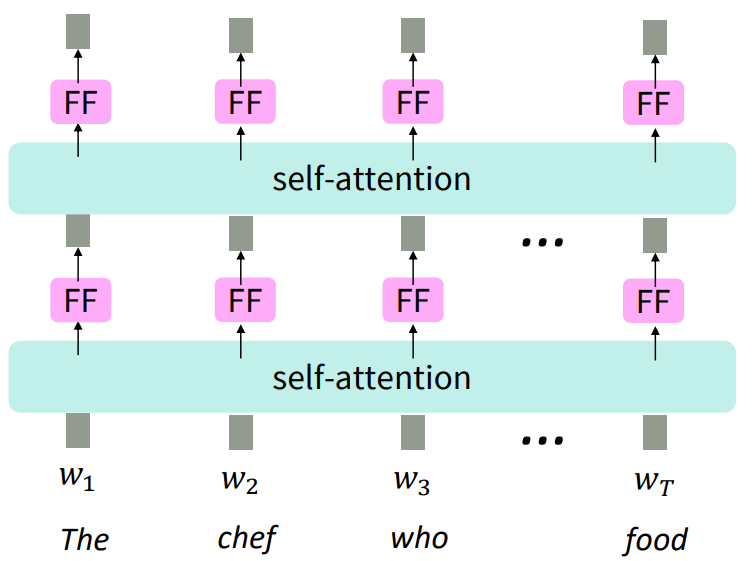
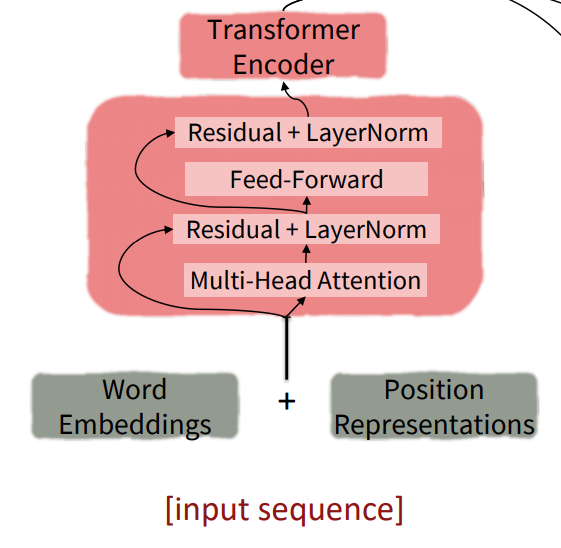
여기까지 transformer의 encoder 구조에 대해 알아봤다.
아래 그림은 encoder의 구조를 시각화 했다.
decoder
- masked attention
decoder에서 단어를 예측할 때 미래 단어를 보고 예측하게 된다.
이를 막기 위한 방법을 소개한다.
나중에 추가… - cross-attention
나중에 추가…
attention vs self-attention
이 부분은 stackexchange를 참고했다.
나중에 추가…
transduction model
나중에 추가…
implementation
나중에 추가…