Week04 Day18

하… 또 밀렸다…

sequence to sequence

sequence to sequence 모델은 대표적인 many-to-many 모델이다.
즉, 입력과 출력이 sequence인 모델이다.
이 모델은 encoder와 decoder로 구성되며 대표적으로 활용되는 task는 machine translation이 있다.
encoder와 decoder는 따로 존재하며 parameter를 공유하지 않는다.
sequence를 입력으로 받으므로 encoder와 decoder는 RNN을 사용하며 cell은 LSTM이다.
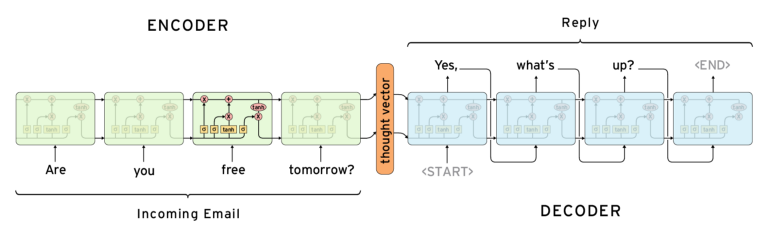
sequence to sequence 모델의 구조는 아래 그림과 같다.
¹
이전 강의에서 설명했듯이 텍스트 데이터를 token으로 나누어 모델에 입력한다.
이 모델에서 사용하는 special token은 <SOS>(Start Of Sentence) 혹은 <BOS>(Beginning Of Sentence), <PAD>, <EOS>(End Of Sentence)가 있다.

<PAD>
이전 강의에서 padding에 관한 설명과 일치한다.
<SOS>
문장의 시작을 알리는 token이다.
decoder에서의 역할은 encoder에서 생성된 hidden state와 함께 첫번째 token을 예측할 때 사용된다.
만약 decoder의 처음 시작을 <SOS>가 아닌 원래 문장의 첫번째 token을 입력한다면 두번째 token부터 예측할 것이다.
그렇게 되면 문장을 예측할 때 첫번째 token을 제대로 예측하지 못하게 된다.
<EOS>
문장의 끝을 의미하는 token이다.
decoder에서의 역할은 token을 언제까지 예측할지를 알려준다.
이 token이 예측된다면 token 예측을 종료한다.

그럼 encoder와 decoder에 대해 알아보자.

encoder
입력 sequence를 받아서 그에 대한 hidden state를 생성한다.
마지막 time step에서 생성되는 hidden state는 입력 sequence의 모든 정보를 담고 있다.
이 벡터를 decoder에서 사용하며 context vector 혹은 thought vector라 부른다.
즉, encoder의 목적은 입력에 대한 정보를 담은 vector 생성이며 출력은 사용하지 않는다.
그리고 입력 sequence의 마지막에 <EOS> token과 seqeunce 길이를 일정하게 하기 위한 <PAD> token을 추가한다.
decoder
encoder에서 넘어온 hidden state와 <SOS> token을 입력하여 출력 sequence의 첫번째 token을 예측한다.
encoder hidden state의 초기값은 zero vector이다.
하지만 decoder hidden state 초기값은 encoder에서 생성한 context vector이다.
그럼 첫번째 예측한 token을 두번째 time step의 입력으로 넣는다.
이 과정을 예측한 token이 <EOS>일 때까지 반복한다.
여기서 문제가 있는데, 초기 학습에는 token을 잘 예측하지 못한다.
잘못된 token이 입력으로 들어가면 잘못된 token을 예측하므로 학습이 어렵다.
따라서 학습할 때는 정답 token을 넣어준다.
하지만 inference 과정에서 학습 데이터에 없는 데이터를 입력으로 넣으면 결과가 좋지 못하다.
그래서 학습할 때 초기에는 정답을 입력하고 어느정도 학습되면 예측된 token을 입력으로 사용한다.

입력 sequence와 출력 sequence 길이가 달라도 된다.
어쩌면 달라야 하는게 맞다.
예를 들어 나는 학생입니다 가 입력이고 출력이 i am a student 라면 입력, 출력의 길이는 2, 4이다.
출력이 입력과 같은 길이라는 것을 보장 못한다.

이 모델의 문제점을 다음과 같다.
encoder, decoder는 RNN 구조이다.
sequence의 길이가 길면 gradient가 점점 작아지는 문제를 개선했지만 완벽하게 해결한게 아니다.
즉, long-term dependency가 있다.
LSTM, GRU를 사용해서 이 문제를 개선했다고 해도 여전히 긴 sequence에 대해 처음 부분 입력에 대한 정보는 소실된다.
또한 encoder에서 입력 sequence의 많은 정보를 이 고정된 길이의 context vector에 담는 bottleneck 현상이 발생한다.
예측할 때 첫 단어가 중요한데 이러한 문제들로 인해 첫 단어의 품질이 좋지 않다.
그러니 문장 전체 품질도 낮아진다.
다음으로 소개하는 모델은 이런 bottleneck 현상을 개선하기 위해 도입되었다.

seq2seq with attention ²

이 모델은 앞서 설명한 seq2seq 모델의 2가지 단점, long-term dependency와 bottleneck 현상, 을 개선하였다.

위 그림은 decoder가 token을 예측하는 4단계를 설명한다.

decoder의 hidden state와 encoder의 모든 time step에서 예측한 hidden state와 dot product를 계산한다.
이를 attention score라 한다.
계산한 dot product에 대해 softmax를 계산한다.
이를 attention distribution이라 한다.
이 attention distribution과 encoder의 모든 hidden state의 가중합을 구하고 이를 attention output이라 한다.
attention output과 decoder의 hidden state를 concatenation을 하고 token을 예측한다.
<EOS> token을 예측할 때까지 1 ~ 4 과정을 반복한다.

위의 1 ~ 3 과정은 token을 예측할 때 입력 token에 중요성을 부여하는 것이다.
다시 말해, attention은 alignment하는 것으로 생각할 수 있다.
위키피디아의 attention에 대한 설명은 다음과 같다.

in the context of neural networks, attention is a technique that mimics cognitive attention.
The effect enhances the important parts of the input data and fades out the rest.
Which part of the data is more important than others depends on the context and is learned through training data by gradient descent.³

attention은 cognitive attention을 모방한 기술이며, input data의 어떤 부분이 중요한지 안한지를 알 수 있다.
뭐가 중요한지는 문맥에 의존하고 gradient descent에 의해 학습된다.
attention의 좀 더 일반적인 정의는 다음과 같다.

Given a set of vector values, and a vector query, attention is a technique to compute a weighted sum of the values, dependent on the query.

value vector 집합과 query vector가 주어져서 query vector에 따라 value vector들의 가중합을 계산하는 것이다.
위에서 설명한 attention에서 value vector 집합은 encoder의 hiddens state에 해당하고 query vector는 decoder의 hidden state에 해당한다.
attention에 대한 intuition은 다음과 같다.

The weighted sum is a selective summary of the information contained in the values, where the query determines which values to focus on.

Attention is a way to obtain a fixed-size representation of an arbitrary set of representations (the values), dependent on some other representation (the query).

가중 합은 query가 어느 value에 초점을 맞춰야 할지 결정하여 value들에 담긴 정보를 선택적으로 요약하는 것이다.
attention은 다른 어떤 representation에 따라 임의의 representation 집합의 고정크기의 representation을 얻는 방법이다.

다음은 attention score의 변형이다.⁴

Notation
$h_i$: $i$ 번째 time step의 encoder hidden state vector, $h_i \in \mathbb{R}^{d_1}$, $d_1$: encoder hidden state vector dimension.
$s$: decoder hidden state vector, $s \in \mathbb{R}^{d_2}$, $d_2$: decoder hidden state vector dimension.
$e_i$: $i$ 번쨰 attention score, $e \in \mathbb{R}^N$
basic dot-product attention: $e_i = s^Th_i \in \mathbb{R}$
위에서 설명한 방법이다.
multiplicative attention: $e_i = s^TWh_i \in \mathbb{R},\ W \in \mathbb{R^{d_2 \times d_1}}$
이 방법은 basic dot-product를 좀 더 일반화한 것으로 hidden state vector의 특정 i, j번째 부분에 가중치를 주는 것이다.
또한 두 hidden state vector의 차원이 달라도 계산할 수 있다.
concat attention: $e_i = v^Ttanh(W[h_i;s]) \in \mathbb{R},\ W \in \mathbb{R^{d_3 \times (d_1+d_2)}},\ v \in \mathbb{R^{d_3}}$
$h_i$ 와 $s$ vector를 concatenation하고 $d_3$ 차원으로 선형변환하고 비선형함수 $tanh(x)$ 를 사용했다.
그리고 scalar 값으로 만들기 위해 $d_3$ 차원의 vector $v$ 와 내적하였다.

attention에 대해 정리해보면 다음과 같다.

NMT(Neural Machine Translation) 분야의 성능을 상당히 향상시켰다.
- decoder가 input data의 어떤 부분을 봐야하는지 알 수 있다.
bottleneck 문제를 개선했다.
- decoder가 직접 input data의 중요한 부분을 찾는다.
gradient vanishing 문제를 개선했다.
- loss에서 encoder의 parameter로 backpropagation할 때 decoder를 거치지 않고 바로 encoder로 간다.
약간의 해석력(interpretability)를 제공한다. ⁵
위 그림의 x축, y축은 영어와 프랑스어이며 단어 간 attention distribution을 나타낸다.
어두울수록 attention score가 낮다.
- attention distribution을 보면 token을 예측할 때 어떤 input data의 정보를 많이 반영하는지 알 수 있다.
  불필요한 데이터를 건너뛴다.
- 명시적으로 input data의 alignment를 알려줘서 학습하는게 아니라 스스로 학습한다.