웹 페이지와 그래프
다음 코드는 한 웹 페이지의 html 일부분이다.
<p class="con">
<a href="/news/newsRead.nhn?type=headline&prsco_id=008&arti_id=0004547213" class="NPI=a:contents,i:0004547213">당정이 2·4 대책 후속 법안을 사실상 확정한 가운데...</a>
<span>머니투데이</span>
</p>
위 코드를 보면 <a> tag는 다른 웹 페이지로 연결해주는 역할을 하며 이를 하이퍼링크라 부른다.
즉, html은 다른 웹 페이지를 가리키는 경우가 많다.
웹 페이지를 정점이라 보면 한 웹 페이지가 다른 웹 페이지를 가리키므로 방향이 있는 간선이 존재한다.
즉, 웹 페이지는 웹 페이지 간 복잡한 상호작용을 하는 complex system이며 이를 그래프로 나타낼 수 있다.
구글 이전 검색 엔진
웹 페이지를 검색하기 위해 여러 방법이 있었다.
예를 들어 웹 페이지에 카테고리를 분류하는 것이다.
하지만 웹 페이지가 무한정 커지고 카테고리의 종류도 늘어나고 어떻게 분류해야 할지 애매했다.
다른 방법은 검색어를 포함한 웹 페이지를 보여주는 것이다.
하지만 악의적으로 페이지 노출을 위해 내용과 상관없는 단어들을 포함하게 되어 문제가 된다.
이 다음으로 소개할 방법은 신뢰성있는 웹 페이지 검색 방법을 소개한다.
PageRank
PageRank algorithm은 Larry Page의 이름을 따서 만들었다.
PageRank (PR) is an algorithm used by Google Search to rank web pages in their search engine results. PageRank is a way of measuring the importance of website pages.
PageRank works by counting the number and quality of links to a page to determine a rough estimate of how important the website is.
The underlying assumption is that more important websites are likely to receive more links from other websites.1
PageRank는 웹 페이지를 순위 매기기 위해 구글 검색에서 사용한 알고리즘이다.
이 알고리즘은 웹 페이지의 중요성을 측정하는 방법이다.
웹 사이트가 얼마나 중요한지를 대략적으로 추정하기 위해 페이지 수와 연결들의 품질을 계산하는 것으로 동작한다.
근본적인 가정은 중요한 웹 사이트들은 다른 웹 사이트들보다 더 많은 연결을 받을 가능성이 있다.
즉, 연결을 많이 받을수록 중요하다고 가정한다.
하지만 악의적으로 연결을 많이 만들 수 있다.
그래서 중요한 웹 사이트의 연결은 좀 더 가중치를 주는 방식을 사용하자.
정점 $i$ 에 대한 PageRank(이하 PR) score는 다음과 같이 계산된다.
\(PR_i = \sum_{j \in N_{in}(i)}\frac{PR_j}{d_{out}(j)}\)
$N_{in}(i)$ 는 정점 $i$ 로 간선을 보내는 정점들의 집합이다.
$d_{out}(j)$ 는 정점 $j$ 의 간선의 수이다.
예를 들어 아래 그림에 대한 PR을 구해보자.
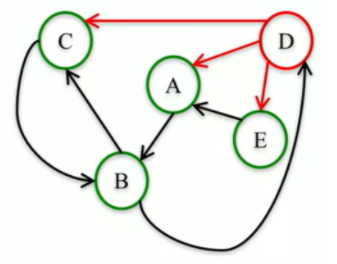
\(PR_A = \frac{PR_D}{3} + \frac{PR_E}{1}\\
PR_B = \frac{PR_A}{1} + \frac{PR_C}{1}\\
PR_C = \frac{PR_B}{2} + \frac{PR_D}{3}\\
PR_D = \frac{PR_B}{2}\\
PR_E = \frac{PR_D}{3}\)
여기서 가정을 하나 추가한다.
웹 사이트 내 하이퍼링크 중 하나를 선택해 이동한다고 하자.
그래서 $t$ 번째 방문한 웹 사이트가 $i$ 일 확률을 $p_i(t)$ 라 하자.
그러면 $p(t)$ 의 차원은 웹 사이트의 수와 같은 확률벡터가 되며 아래 식이 성립한다.
\(p_i(t+1) = \sum_{j \in N_{in}(i)}\frac{p_j(t)}{d_{out}(j)}\)
이때 $t = 0$ 인 경우는 모두 동일하게 $\frac{1}{|V|}$ 로 초기화한다, $|V|$: 모든 정점의 수.
반복적으로 계산하며 나중에 $p(t+1)$ 과 $p(t)$ 의 차이가 작을 때 반복을 그만한다.
하지만 문제가 발생한다.
과연 수렴을 보장할 수 있는가에 대한 물음이 생긴다.
이전 강의에서 설명했듯이 간선은 행렬로 표현할 수 있다.
이때 이 행렬을 여기선 전이행렬(transition matrix)라 한다.
전이행렬과 확률벡터의 수렴
나중에 추가…
문제점과 해결
수렴이 안될 때를 해결하기 위해 순간이동(teleport)를 도입한다.
만약에 현재 정점에 간선이 있다면 일정한 확률로 간선 중 하나를 균일한 확률($\alpha$)로 이동하거나 임의의 정점으로 이동한다.
혹은 간선이 없다면 임의의 정점으로 이동한다.
그래서 아래는 최종 PR score를 구하는 수식이다.
\(p_i(t+1) = \sum_{j \in N_{in}(i)} \alpha\frac{p_j(t)}{d_{out}(j)} + (1-\alpha)\frac{1}{|V|}\)
사실 $(1-\alpha)$ 를 고정하여 사용하면 막다른 간선문제를 해결할 수 없다.
그래서 이 문제를 해결하기 위해 다음과 같이 두 단계로 나누어 $p_i(t+1)$ 를 계산한다.
- $p_i(t+1) = \sum_{j \in N_{in}(i)} \alpha\frac{p_j(t)}{d_{out}(j)}$
$S = \sum_{i \in V}p_i(t+1)$ -
$p_i(t+1) = p_i(t+1) + \frac{1-S}{ V }$
metaclass
나중에 추가…
