Week05 Day24

이번 학습정리는 BoostCamp 강의와 CS224W을 바탕으로 했다.

graph representation

graph에 대한 전통적인 machine learning은 graph를 입력으로 넣고 node, edge, graph level에서 feature를 추출(feature engineering)한다.
그리고 feature들을 label로 mapping하는 모델을 학습한다.
매번 모델을 만들 때마다 feature engineering을 해야된다.
graph representation learning은 매번 feature engineering하는 고통을 덜어준다.
한번 만든 graph representation은 여러 task에서 사용할 수 있다, node classification, Link prediction, graph classification, anomalous node detection, clustering 등 graph의 feature가 필요한 task라면 상관없다.
그래서 graph representation의 목표는 task와 상관없이 graph에 대한 machine learning을 위한 효율적인 feature learning이다.
즉, 우리가 필요한 건 각 task에 맞는 고유하고 특수한 graph representation learning이 아니라 범용적으로 모든 task에서 사용할 수 있는 graph representation learning이다.

node embedding

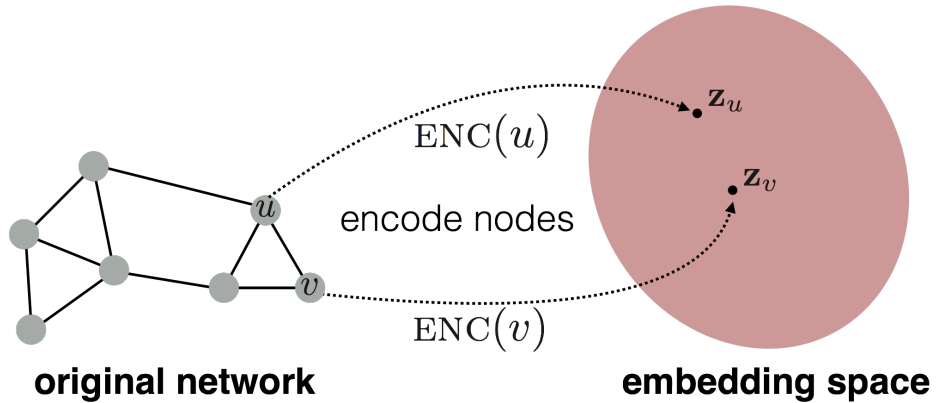
여기서는 node를 $\mathbb{R}^d$ 로 변환하는 node embedding에 대해 알아본다.
graph에서 가까운 관계인 두 정점을 $\mathbb{R}^d$ 로 변환했을때 가까이 위치하게 만들고 싶다.
¹
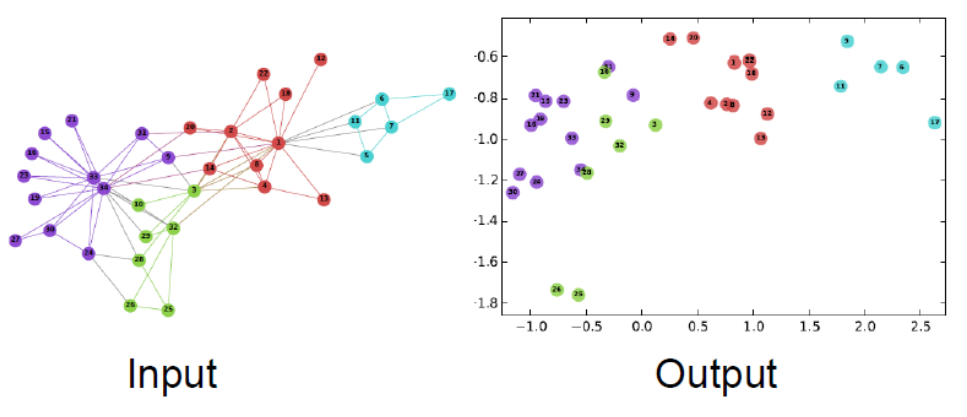
위 그림의 왼쪽은 graph에서 가까운 정점을 색깔별로 표시했다.
오른쪽은 $\mathbb{R}^2$ 로 변환한 모습이다.
보면 graph에서 가까운 정점은 $\mathbb{R}^2$ 에서도 가까이 변환된 것을 확인할 수 있다.

setup

다음을 만족하는 graph $G$ 가 있다고 하자
$V$ : 정점들의 집합
$A$ : 인접행렬(adjacency matrix), 각 원소는 binary이다.
간단하게 하기 위해 node feature나 그 외 정보는 없다고 가정한다.

goal

$\mathbb{R}^d$ 공간에서 graph에서의 similarity가 보존되는 정점들에 대한 embedding을 찾자.
그러기 위해서는 graph에서 두 정점이 유사하다(similar) 라는 것에 대한 정의와 encoding을 어떻게 할 것인지가 필요하다.
먼저 encoding에 대해 알아본다.

shallow encoding

encoding의 가장 간단한 방법은 한 정점에 대응하는 $\mathbb{R}^d$ 벡터를 사용하는 것이다.
이 방법은 word2vec을 공부했던 내용과 비슷하다.
그래서 자세한 설명은 생략하겠다.
이에 대한 notation은 다음과 같다.
$Z \in \mathbb{R}^{|V| \times d}$ : embedding matrix
$z_v$ : 정점 $v$ 에 대한 embedding vector
objective는 유사한 두 정점 $u, v$ 에 대해 $z_v^Tz_u$ 를 최대화하는 것이다.
참고로 여기서 decoder는 두 embedding vector의 dot product이다($DEC(z_u,\ z_v) = z_v^Tz_u$).

how to define similarity

두 정점이 유사하다 라는 것을 어떻게 정의할까?
만약 두 정점이 연결되거나 이웃을 공유하거나 유사한 구조적인 역할을 갖는다면 유사한 embedding을 가져야 할까?
random walk라는 방법으로 정점의 유사도를 정의할 것이다.

DeepWalk

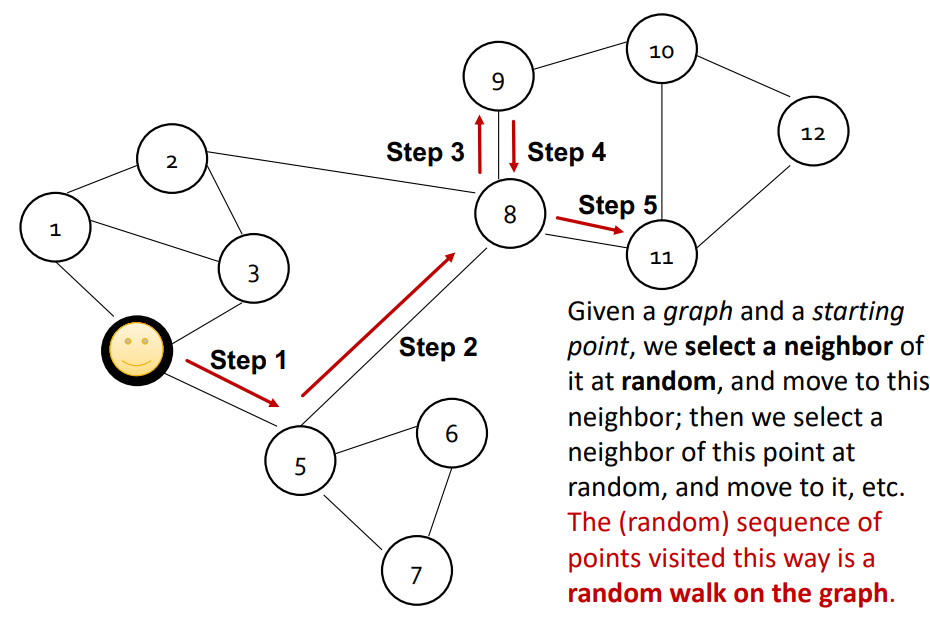
graph가 주어지고 어떤 정점 $v$ 에서 출발한다.
정점 $v$ 의 이웃을 임의로 선택하여 이동한다.
다시 그 정점의 이웃을 임의로 선택하여 이동한다.
이 과정을 반복한다.
나중에는 이 방식으로 방문한 정점들의 sequence를 얻을 수 있고 이걸 random walk라 한다.
이 때 시작한 정점 $v$ 의 embedding $z_v$ 에 대해 정점 $u$ 를 방문할 확률은 $P(u|z_v)$ 라 한다.
확률을 예측하기 위해 비선형 함수 softmax, sigmoid를 사용한다.

random walk의 좀 더 자세한 과정은 다음과 같다.

정점 $v$ 에서 시작하여 random walk로 정점 $v$ 를 방문할 확률을 추정한다.
embedding space에서 similarity는 random walk의 similarity를 근사하다고 가정하고 embedding vector를 최적화한다.

why random walk

표현성(expressivity)
지역적이고 높은 차수의 이웃 정점들의 정보를 포함하는 node similarity의 유연한 확률적(stochastic) 정의이다.
중요한 가정은 정점 $u$ 에서 출발하여 random walk로 정점 $v$ 를 방문한다면 $u, v$ 는 유사하다고 본다.
효율성(efficiency)
학습할 때 모든 정점쌍을 고려하지 않아도 된다.
오직 random walk로 방문한 정점들을 고려하면 된다.

random walk optimization

notation은 다음과 같다.
$N(u)$ : random walk로 얻은 정점 $v$ 의 이웃 정점 집합(random walk로 정점 $v$ 에서 시작하여 방문한 정점 집합)
log-likelihood objective : $\sum_{u \in V}logP(N(u)|z_u)$

최적화 과정은 다음과 같다.

정점 $u$ 에서 시작하여 고정된 횟수의 random walk로 방문한 정점들을 구한다.
방문한 정점들의 집합 $N(u)$ 를 얻는다, 이때 중복된 정점이 있을 수 있다.
$\sum_{u \in V}logP(N(u)|z_u)$ 를 최대화하는 embedding을 찾는다.
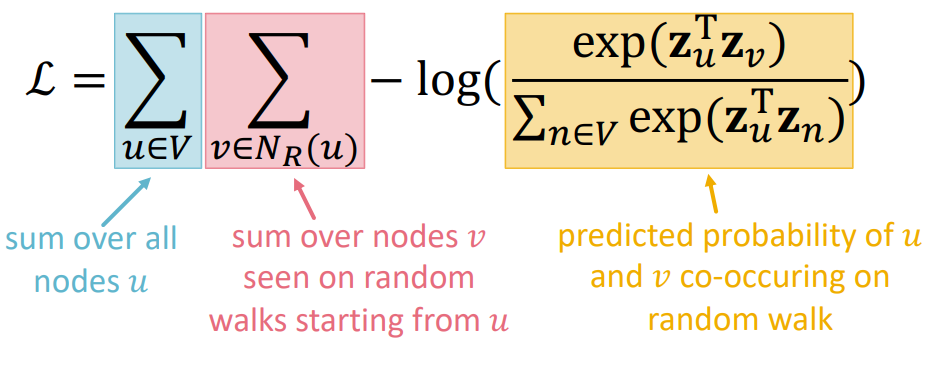
log-likelihood objective는 $\sum_{u \in V}\sum_{v \in N(u)}-logP(v|z_u)$ 로 다시 쓸 수 있다.

그럼 $P(u|z_v)$ 를 좀 더 살펴보자.
$P(u|z_v) = exp(z_u^Tz_v) / \sum_{n \in V}exp(z_u^Tz_n)$ 정점 $v, u$ 가 유사하기 때문에 $z_u^Tz_v$ 값이 높길 원한다.
즉, $P(u|z_u)$ 가 높다는 것은 모든 정점들의 embedding과 $z_u$ 와의 유사도 중 $z_v$ 와 유사도가 가장 높다는 뜻이다.
위 수식을 softmax라 한다.

최종적으로 수식을 다시 쓰면 위 그림과 같고 $\mathcal{L}$ 을 최소화하는 $z_u$ 를 찾는 것이다.
하지만 위 수식의 문제점은 계산량이다.
잘보면 $exp(z_u^Tz_n)$ 을 $|V|^2$ 번 계산한다.
softmax는 많은 정점에 대해 계산량이 제곱으로 증가하므로 이를 대체할 방법이 필요하다.

negative sampling

이 논문에 의하면 $log(exp(z_u^Tz_v) / \sum_{n \in V}exp(z_u^Tz_n))$ 를 $log(\sigma(z_u^Tz_v)) - \sum_{i=1}^k log(\sigma(z_u^Tz_{n_i})),\ n_i \sim P_V$ 로 근사할 수 있다고 나온다.
논문을 좀 더 읽어보고 내용을 추가하겠다.

여기서 $k$ 는 negative sample 의 수이다.
$k$ 가 높을수록 강건한(robust) 추정치를 얻을 수 있지만 negative event에 대해 높은 bias가 생길 수 있다.

node2vec

node2vec은 여태까지 배운 random walk 방법이 너무 단순해서 similarity의 개념이 제한적이라는 문제를 갖고 있다.
node2vec은 다른 방법을 제안한다.
역시 node2vec의 목표도 graph에서 가까운 정점을 보존하여 embedding space에서도 가깝게 하는 embedding을 찾고 싶다.
기존 방법과 차이는 정점 $u$ 에서 시작하여 방문하는 정점들을, $N(u)$, 다르게 하여 좀 더 좋은 embedding을 얻는 것이다.

biased random walk

²
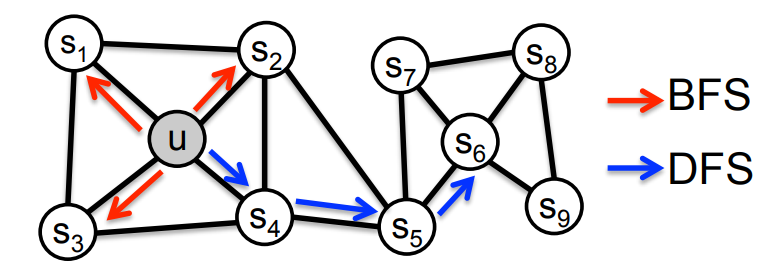
기존 방법은 한 정점의 이웃 정점을 임의로 방문했다.
여러 이웃 정점 중 동일한 확률로 방문하기 때문에 편향이 없었다.
하지만 biased walk는 편향이 있다.
위 그림을 보면 이웃 정점을 방문할 때 가까운 이웃을 먼저 방문할 것인지(BFS) 먼 이웃을 먼저 방문할 것인지(DFS)를 나타낸다.
이것은 local과 global 관점 사이에서 trade off가 있다.
예를 들어 local 위주로 방문한다면 방문하는 정점들은 $s_1,\ s_2,\ s_3$ 이 되고 global 위주라면 $s_4,\ s_5,\ s_6$ 이 된다.
그럼 좀 더 방문하는 방법에 대해 알아보자.

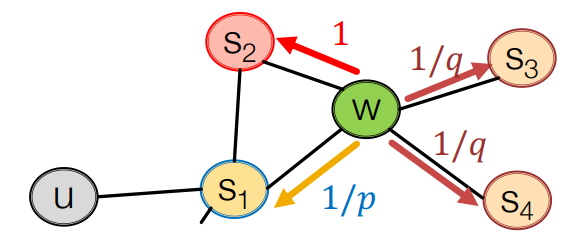
위 그림에서 정점 $u$ 에서 시작하여 $s_1$ 을 방문하였고 현재 $w$ 에 있다.
$w$ 에서 방문할 수 있는 정점은 $s_1, s_2, s_3, s_4$ 이다.
이때 $w$ 이전에 방문한 $s_1$ 를 고려하여 $s_1$ 를 다시 방문할 확률은 $1/p$ 이며 $s_2$ 는 1이다.
$s_1$ 의 이웃과 $w$ 의 이웃이 같은 정점에 대해 1을 부여한다.
$w$ 의 또다른 이웃인 $s_3,\ s_4$ 는 $s_1$ 과 멀어지는 정점이므로 $1/q$ 를 부여한다.
$1/p,\ 1,\ 1/q$ 는 정확히 확률은 아니고 normalization을 해야된다.
$p$ 는 각각 이전 정점으로 돌아가는 정도, $q$ 는 이전 정점에서 멀리 벗어나는 정도를 의미한다.
만약 BFS처럼 탐색하고 싶다면 $p$ 를 줄이고 DFS처럼 탐색하고 싶다면 $q$ 를 줄이면 된다.
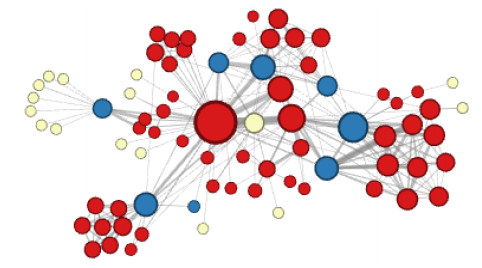
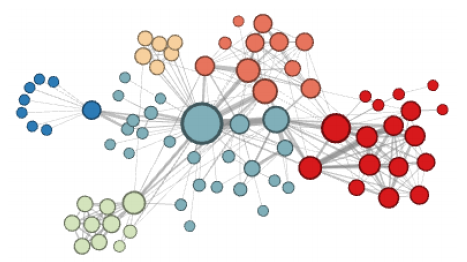
아래 두 그림은 embedding을 한 후 k-means를 시행하여 같은 군집은 같은 색을 나타낸다.

위 그림은 먼 정점에 높은 확률을 준 경우이다.