Week05 Day25

이번 학습정리는 BoostCamp 강의와 CS224W을 바탕으로 했다.

Recapitulation

이전강의에서 node embedding(혹은 shallow embedding)을 배웠다.
이 방법은 transductive learning으로 몇가지 한계가 있다.

• $O(|V|)$ 만큼 parameter가 필요하다.
  node간 parameter를 공유하지 않는다, 즉 모든 node는 고유한 embedding을 가진다.
• 내재적으로 transductive하다.
  학습 데이터에 없는 node에 대해 embedding을 생성할 수 없다.
• node feature들을 통합하지 않는다.
  많은 graph들은 활용할 수 있고 그래야만 하는 feature들을 가지고 있다.

위와 같은 한계점을 개선한 방법인 GNN(Graph Neural Network)에 대해 알아본다.

GNN(Graph Neural Network)

Many underlying relationships among data in several areas of science and engineering, e.g., computer vision, molecular chemistry, molecular biology, pattern recognition, and data mining, can be represented in terms of graphs.
In this paper, we propose a new neural network model, called graph neural network (GNN) model, that extends existing neural network methods for processing the data represented in graph domains.
This GNN model, which can directly process most of the practically useful types of graphs, e.g., acyclic, cyclic, directed, and undirected, implements a function $\tau(G,n) \in \mathbb{R}^m$ that maps a graph G and one of its nodes n into an m-dimensional Euclidean space.¹

여러 과학, 공학분야에서, 예를 들어 컴퓨터 비전, 분자화학, 분자생물학, 패턴인식, 데이터 마이닝, 데이터 사이에 많은 근본적인 관련성들은 graph 관점에서 표현될 수 있다.
이 논문에서는 새로운 신경망 모델인 GNN(Graph Neural Network) 모델을 제안한다, graph domain에서 표현되는 데이터를 처리하기 위해 기존 신경망 방법들을 확장한 것이다.
이 GNN 모델은, graph의 유용한 여러 형태들, 예를 들어 비순환, 순환, 유향, 무향, 중 대부분을 직접 처리할 수 있다, n개의 node들을 m차원의 Euclidean space로 mapping하는 함수를 구현할 수 있다.

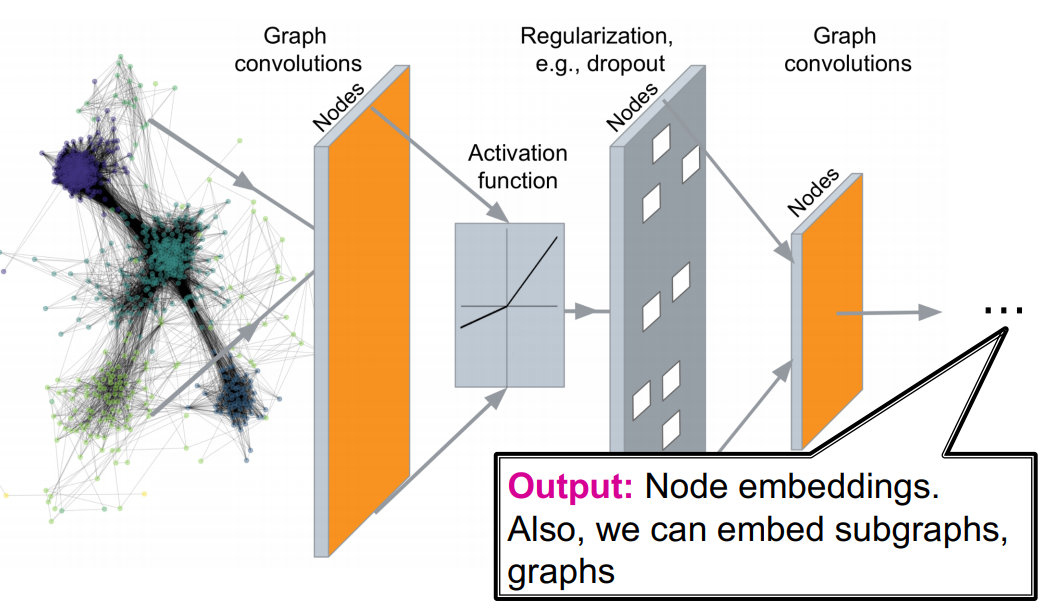
graph 구조에 기반하여 비선형변환을 여러개 쌓아서 정점을 m차원의 벡터로 embedding하는 방법을 살펴볼 것이다.
먼저 그래프 $G$ 를 아래와 같이 가정할 것이다.

• $V$ : 정점 집합, $v$ : 정점, $N(v)$ : 정점 $v$ 의 이웃 정점들의 집합
• $A$ : 인접행렬(adjacency matrix), 각 원소는 binary형태
• $X \in \mathbb{R}^{m \times |V|}$ : node feature 행렬
  • node feature
    예를 들어, social network에서는 유저들의 프로필 혹은 유저 이미지이며 biological network에서는 gene expression profiles, gene functional information 등이 해당된다.

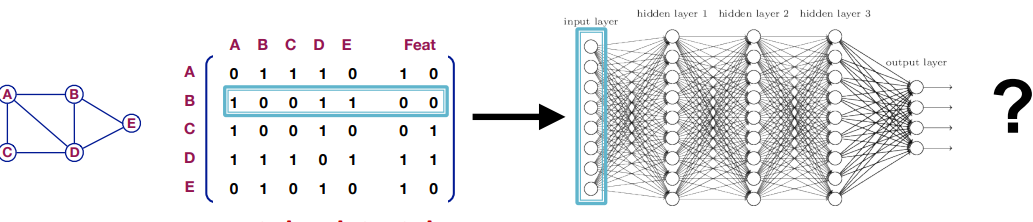
GNN을 만드는 단순한 접근은 인접행렬과 node feature를 신경망의 입력으로 넣는 것이다.
그러나 다음과 같은 문제가 발생한다.

• $O(|V|)$ 개의 parameter가 필요하다.
  • 왜?
• 크기가 다른 graph에는 적용할 수 없다.
  • 위 그림을 예시로 정점의 수가 5개 이고 node feature의 차원이 2이다.
    즉, 입력 차원이 7인 신경망이며 이와 같지 않은 graph에는 적용할 수 없다.
• node 순서에 민감하다.
  • 위 그림은 인접행렬을 A-B-C-D-E 순으로 만들었다.
    만약에 C-D-A-B-E 순으로 인접행렬을 만들어 신경망을 만든다면 다른 결과가 나올 것이다.
    C-D-A-B-E 순으로 인접행렬로 만든다고 해도 graph의 본질이 바뀌는게 아니다.
    즉, 순서를 어떻게 부여하느냐와 상관없이 같은 결과가 나와야 된다.

이런 문제를 해결할 수 있는 아이디어를 소개한다.

GCN(Graph Convolutional Network)

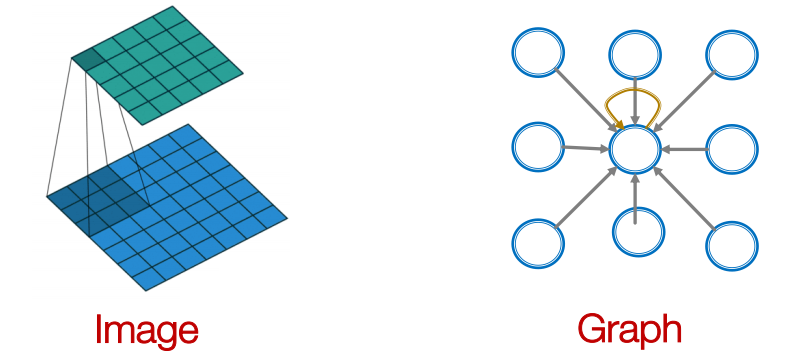
이전에 배운 CNN(Convolutional Neural Network)은 이미지에 사용되는 신경망이었다.
이미지는 격자(grid)형태의 데이터이다.
우리는 node feature를 활용하여 단순 격자형태를 넘어서 convolution을 일반화하고 싶다.
그러나 graph는 고정된 개념의 locality 혹은 sliding window가 존재하지 않는다.
graph는 permutation에 불변하다.

convolution의 kernel은 주변 pixel의 정보를 요약해서 하나의 값으로 바꾼다.
이 idea를 적용하여 한 정점의 주변의 정점들의 정보를 요약하여 해보자.

key idea

즉, 핵심 idea는 주변 network의 이웃들에 기반하여 node embedding을 만드는 것이다.
신경망을 사용하여 한 정점의 이웃들의 정보를 취합한다는 것이다.
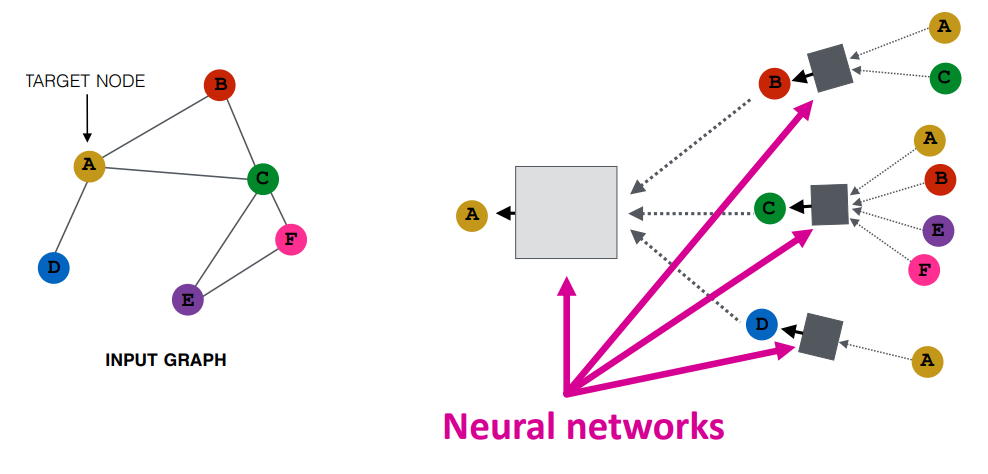
위 그림을 예시로 보면 2층 신경망을 사용하고 정점 $A$ 의 node embedding을 구할 것이다.
$N(A) = B,\ C,\ D$ 이다.
정점 $B, C, D$ 의 정보를 취합하여 정점 $A$ 의 embedding을 생성한다.
정점 $A$ 의 이웃 중 $B$ 의 정보 역시 이웃 정점 $A, C$의 정보를 요약해서 생성된다.
이 과정을 layer 수 만큼 반복한다.
모든 정점들은 이웃 정점에 기반하여 computation graph를 정의할 수 있다.
이를 정의한다면 정보를 어떻게 propagation하는지 학습할 수 있다.

formulation

그럼 수식을 살펴보자.
\(h_v^{l+1} = \sigma(W_l\sum_{u \in N(v)}\frac{h_u^l}{|N(v)|}+B_lh_v^l),\ l \in \{0,\ ...,\ L-1\}\) $L$ : layer 수.
$h_v^0 = X_v$ : 최초 0번째 layer의 node embedding은 node feature이다.
$h_v^l$ : 정점 $v$ 에 대한 $l$ 번째 layer node embedding.
$z_v = h_v^L$ : 정점 $v$ 에 대한 최종 node embedding.
$\sigma(\cdot)$ : 비선형함수를 사용한다.
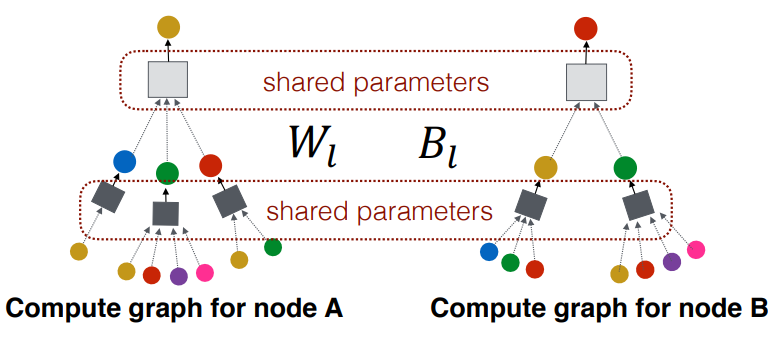
$W_l,\ B_l$ : $l$ 번째 layer의 학습가능한 weight이며 각각 이웃 정점들의 정보 취합(neighborhood aggregation)과 자신의 node embedding의 변형(self transformation)을 의미한다.
궁금한 것은 $h_v^{l+1}$ 을 구하기 위해 $h_v^l$ 을 사용하는 것이다.
이 의문에 대한 대답을 여기서 찾았다.
directed graph에서 이웃의 정의를 나에게 연결이 들어오는 정점으로 한다면(즉, in-neighborhood) in-degree가 0인 정점은 이웃이 없게 되어 embedding이 불가능해진다.
추가적으로 알게 된 점은 이웃 정점의 embedding을 더하고 이웃 수만큼 나누어주는데 나누지 않는다면 이웃이 많은 정점은 그 값이 커질 것이며 gradient가 커지게 된다.
이를 방지하기 위해 이웃 수로 나눈다.
위 수식을 행렬로 표현할 수도 있지만 생략하겠다.

how to train

GNN을 어떻게 학습할까?
우리는 $z_v$ 를 얻었고 두가지 방식으로 학습할 수 있다.

• supervised learning
  \(min_{\Theta}\mathcal{L}(y, f(z_v))\) $y$ : node label
  $\mathcal{L}$ : $y$ 가 real number라면 L2 loss를, categorical이라면 cross entropy를 사용한다.
• unsupervised learning
  이전에 배웠던 deepwalk, node2vec처럼 학습시킬 수 있다.

inductive capability

위 그림은 같은 layer일때 사용하는 parameter가 동일함을 나타낸다.

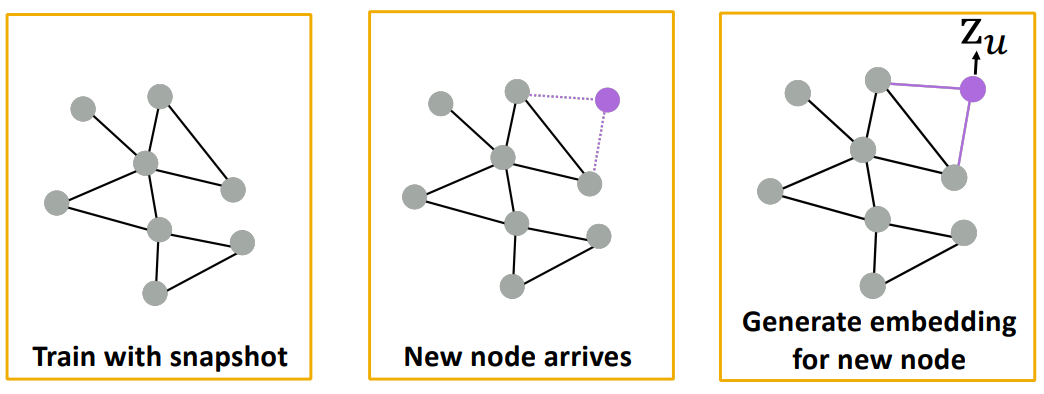
위 그림처럼 학습할 때는 없던 정점이라도 기존 graph의 정점들과 연결되어 embedding을 생성할 수 있다.

GraphSAGE(Graph SAmpling and agGrEgation)²

앞서 살펴본 GCN은 주변 이웃 정점의 정보를 취합하는 방법으로 평균을 사용했다.
여기서는 여러가지 취합하는 방법에 대해 알아본다.
GCN과 차이는 취합하는 방법뿐만 아니라 이웃 정점에도 있다.
이름에서 알 수 있듯이 GraphSAGE는 sampling을 한다.
sampling은 이웃 정점을 선택할 때 사용한다.
만약 한 정점이 나머지 모든 정점과 연결된다면 $N(v)$ 의 크기는 $|V|$ 이다.
또한 연결되는 이웃 정점의 수가 모두 다르므로 학습에 대한 시간복잡도를 계산할 수 없다.
따라서 일정한 수의 이웃 정점을 사용한다.
sampling 방법은 고정된 크기의 uniformly sampling을 한다.

formulation

우리는 $N(v)$ 의 여러 벡터들을 하나의 벡터로 취합하는 미분가능한 함수가 필요하다.
다음은 GraphSAGE의 formulation이며 AGG의 여러 variants를 소개한다.
\(h_{N(v)}^{l+1} = AGG({h_u^l,\ u \in N(v)})\\ h_v^{l+1} = \sigma(W_l \cdot CONCAT(h_{N(v)}^{l+1},\ h_v^l)),\ l \in \{0,\ ...,\ L-1\}\\ h_v^{l+1} = h_v^{l+1} / \parallel h_v^{l+1} \parallel_2\)

• mean : $h_v^{l+1} = \sigma(W_l \cdot MEAN(\lbrace h_v^{l} \rbrace \cup \lbrace h_u^l, u \in N(v) \rbrace))$
• LSTM : $AGG = LSTM([h_u^l,\ u \in \pi(N(v))])$
  LSTM은 larger expressive capability의 장점을 가진다.
  하지만 입력의 순서를 고려하는 모델이다.
  이웃 정점들을 임의로 섞어서 LSTM에 입력으로 넣는 방식을 사용한다.
• pooling : $AGG = max(\lbrace \sigma(W_{pool}h_u^l + b, u \in N(v)) \rbrace)$
  여기서 max는 element-wise로 최대값을 가져온다.
  $\sigma(\cdot)$ 은 non-linear function을 사용한다.
  max pooling을 소개하지만 mean pooling과 별 차이가 없었다고 한다.

how to train

unsupervised learning에서 loss function은 다음과 같다.
\(J_G(z_u) = -log(\sigma(z_u^Tz_v)) -Q \cdot \mathbb{E}_{v_n \sim P_n(v)}log(\sigma(-z_u^Tz_{v_n}))\)
학습은 흡사 node2vec과 유사하다.
$v$ 는 fixed-random walk에서 정점 $u$ 근처에 있는 정점이다.
$\sigma(\cdot)$ 은 sigmoid function을 사용한다.
$P_n$ 분포는 negative sampling distribution이며 $Q$ 는 negative sample 수이다.
supervised learning에서 loss function은 앞서 설명한 것과 같다.

Relation to the Weisfeiler-Lehman Isomorphism Test

논문에 언급되어 있는데 잘 모르겠다..ㅠㅠ
나중에 추가할 수 있으면 해야겠다.

GAT(Graph Attention Network)

나중에 추가…